ReID任务中的CMC和mAP

ReID#

ReID指Re-identification，常翻译为重识别。ReID任务本身分类很多，本文只讨论基于图片的ReID任务中single-gallery-shot这一最简单的情况。

重识别任务可以描述如下：

给定一个Gallery集合\(G\)，包含有\(N\)张图片，分属\(M\)个ID(identity)。给定一张未知ID的图片做query(或者叫probe), 计算出下式的结果：\(max(Similarity(query, g_i)), i\in1,2,3,...,N, g_i\in G\)。得到i之后，图片\(g_i\)对应的ID就是query的ID。大部分ReID相关的研究，都是在研究Similarity()这个函数，使得这个函数在同ID时返回值高，不同ID时返回值低。

下图就是一次典型的重识别任务:

为了更好地理解，我在这篇文中介绍一个新的重识别任务：水果emoji重识别。

我们现有一个水果emoji的数据集\(G\)：[🍍🍎🍎🍏🍍🍏🍎🍏🍍🍍🍍🍏🍎🍏🍍]，假定这个数据集中，即使是相同的emoji，图片也有细小的差别。数据集一共包含\(N=15\)张图片，共有\(M=3\)种ID。任意给定一组query: [🍎,🍏]，从数据集\(G\)中找到和每个query最相近的5张图片(为了保证准确率，我们都是返回一组最相近的图片，而不是如前文所述的单独一张图片)。

我们现在有两个评价emoji之间相似程度的函数Similarity1()和Similarity2()。对于query🍎，Similarity1()得到[🍍🍎🍎🍎🍏]，Similarity2()得到[🍎🍍🍎🍎🍏]。对于query🍏，Similarity1()得到[🍏🍎🍍🍏🍏]，Similarity2()得到[🍎🍏🍏🍏🍍]。得到的结果都按与query的相似度从左至右排列。那么Similarity1()和Similarity2()哪个得到的结果更好呢？

或者说：我们应该怎么度量Similarity()函数的性能？答案就是CMC和mAP。

CMC#

CMC是Cumulative Matching Characteristics的缩写，我个人把它翻译为累计匹配特性。ReID模型的好坏可以通过CMC曲线来评价。为了计算CMC曲线，首先要把每次查询的结果按相似程度排序。接着，引入一个概念: \(topK\)准确度: \(AccK\)，其计算公式如下：

\[ AccK= \begin{cases} 1& \text{前K个结果中有同ID的结果}\\ 0& \text{前K个结果中没有同ID的结果} \end{cases} \]

这里的K是一个从1开始增加的变量。显然，\(AccK\)形同单位阶跃函数。假设在查询得到的结果中，与query同ID的结果第一次出现时的排名为\(F\)，那么显然，\(AccK\)在\(K=F\)时，值由0变为1。 CMC曲线的计算方法就是，把每个query的\(AccK\)曲线相加，再除以query的总数，即平均\(AccK\)曲线。

回到我们的水果emoji重识别任务。分别计算两个query的AccK曲线如下：

Similarity    1          2
query🍎: 0 1 1 1 1 | 1 1 1 1 1
query🍏: 1 1 1 1 1 | 0 1 1 1 1

再平均各个query的AccK曲线，由此我们得到这两种相似度函数的CMC曲线都是[0.5，1，1，1，1] 由于query只有两个，所以得到的CMC的值有些简单。但是当query数足够大时，CMC曲线就会变成下图这样：

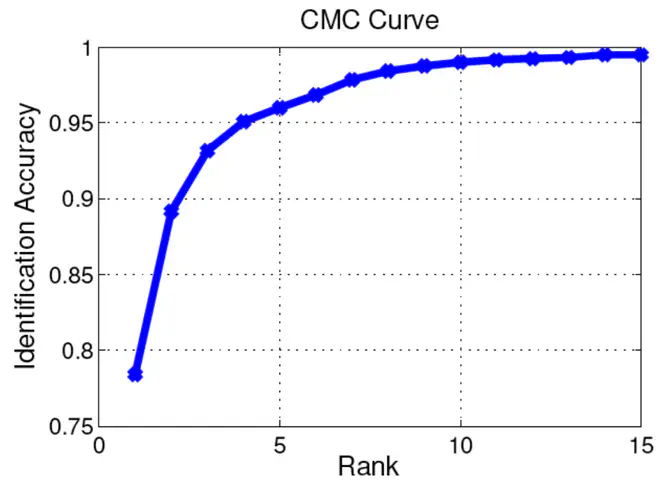
由于AccK曲线是一个单位阶跃函数，CMC曲线必定是一个单调递增的曲线。曲线上某个点如(R5, 0.96)就表示正确结果在前返回所有结果中排名前5的准确率能达到96%。实际论文中，常取CMC曲线上的某几个点之间对比，比如常出现的Rank1，Rank5，就分别是CMC曲线上，K=1，5时的值。

mAP#

mAP是mean Average Precision的缩写。mAP涉及到的前置概念比较多：mAP是每个query的AP(Average Precision)的平均值，而AP又指Precision(准确率，又称查准率)的平均值。我们从头开始讲起。

对于ReID任务，我们经常关心两个问题：

查询得到的结果中，和查询图片同一ID的结果占比多少?
同一ID的图片中，有多大比例的图片被检索出来了?

这两个问题分别对应查准率(precision)和查全率(recall)，亦称作准确率和召回率。因为准确率这个称呼在别的领域有其它意义，为了防止误解，我还是喜欢用查准率和查全率的说法。

查准率和查全率#

查准率就是和query同一ID的图片在查询结果中的占比。计算公式如下:

\[ precision = \frac{\mid\{同ID图片\}\cap\{查询结果\}\mid}{\mid\{查询结果\}\mid} \]

查准率可以同时考虑所有的获取到的结果，也可以单独给定一个特定的值K，只考虑返回结果中排名前K的查询结果，在这种情况下，查准率又可以称为前K查准率，记作P@K。

查全率就是和query同一ID的图片出现在查询结果中的数量占总数的比例。计算公式如下：

\[ recall = \frac{\mid\{同ID图片\}\cap\{查询结果\}\mid}{\mid\{同ID图片\}\mid} \]

查准率和查全率看上去都很有意义，但我们能直接用它俩来评判ReID模型的性能了吗？当然不行，由于查准率和查全率都是通过比例来计算，完全忽略了返回结果的排序！当查询🍏时，返回🍏🍏🍏🍎🍍和🍎🍍🍏🍏🍏当然是不一样的，但其查准率和查全率却是一样的。返回结果的顺序被忽略了。

值得注意的是，查准率和查全率是一个相互矛盾的度量，比如为了增加查全率，我们可以通过增加查询结果的数量来实现，当查询结果数量等于数据集大小时，查全率一定等于1，因为这时所有图片都被查询得到了。但此时查准率就成了最小值。所以比较模型的性能不是那么简单的事情。

P-R曲线图#

那怎么比呢？肉眼比对时，我们常从结果的第一个开始，一个一个比对。借鉴这种思路，我们可以逐渐增加查询结果的数量，从第一个开始，一直到系统给出的查询结果的最后一个，把中间每个点对应的查准率和查全率计算出来然后绘制到一张图上。

我们接着拿水果emoji重识别任务做例子，对于query🍏，Similarity1()得到[🍏🍎🍍🍏🍏]，Similarity2()得到[🍎🍏🍏🍏🍍]。我们现在首先绘出此时两种方法的P-R曲线。注意，由前文的任务定义得\(\mid\{同ID图片\}\mid=5\)

序号	Similarity1		Similarity2
	查全率	查准率	查全率	查准率
1	0.2	1	0	0
2	0.2	0.5	0.2	0.5
3	0.2	0.33	0.4	0.66
4	0.4	0.5	0.6	0.75
5	0.6	0.6	0.6	0.6

接着将这些点绘制在一张图上：

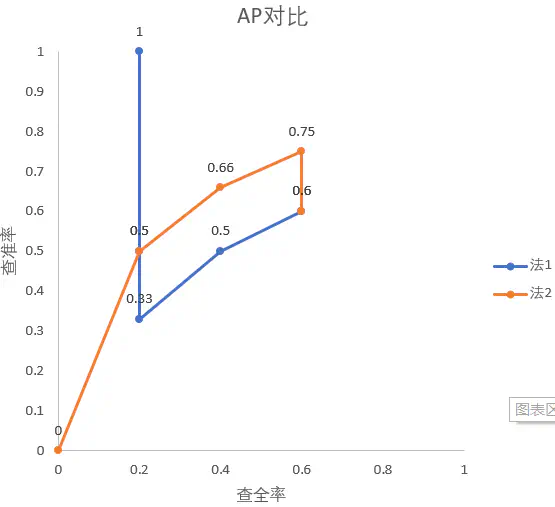
由于5个点太少，上图中曲线还没表现出明显的趋势。实际上，在查询量足够大时，P-R图一般都类似于下图：

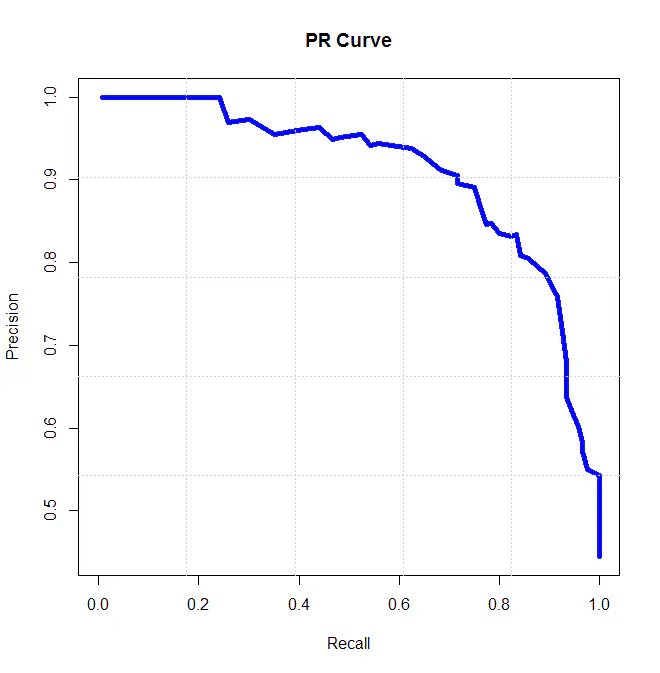
P-R图直观地显示出了ReID模型的查全率和查准率，显而易见，如果一个模型的P-R曲线包住了另一个模型的P-R曲线，这个模型的性能就好于另一个模型。

Average Precision#

显然，PR曲线与坐标轴围起来图形的面积一定程度上反应了ReID模型的性能，我们把这个面积叫做Average Precision。这个面积怎么求？由积分知识可得:

\[ AveP = \int_{0}^1p(r)dr \]

可惜，我们得到的是曲线上一个个点，得不到\(p(r)\)的准确公式，没法用上面的公式计算。但计算AP的过程已经可以被归结为这么一个问题：

假设一共返回\(N\)个查询结果，计算N个点\(\{(recall_k, precision_k), k\in1,2,3,...,N\}\)的离散积分。

显然，可以用多个长方形条的面积之和表示积分结果。

\[ AveP = \sum_{k=1}^{N}precision_i(recall_k-recall_{k-1}) \]

拿水果emoji重识别中的查询为🍏时的Similarity1做个例子：

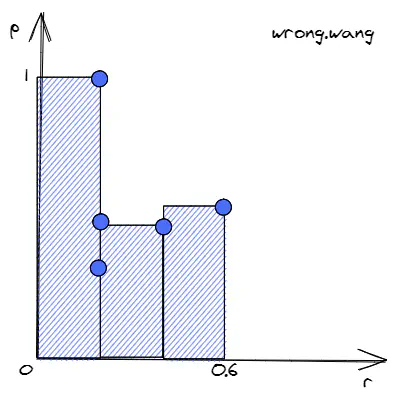
注意，图中r一致，p在变小的前3个点中，只有p最大的点对计算积分值有影响。因为只有此时\(recall_k-recall_{k-1}\)值不为0。这样，我们得出一个结论，计算积分时，只需要考虑查准的结果处(假设为第\(k\)个查询结果)对应的\((recall_k, precision_k)\)。

可以这么理解，返回结果[🍏🍎🍍🍏🍏]中第2，3个结果都没查准，那么前2，3个结果中查准个数不变，即recall保持不变，recall保持不变意味着这几个点在P-R图中，位于同一条平行于p轴的直线上。由于\(recall_k-recall_{k-1}=0\)，它们不影响积分结果。

所以如果令集合\(\Omega\)为和query同ID的第k个查询结果的集合，\(N_t\)为所有与查询图片同ID的图片数目，\(\Delta recall=1/N_t\)：

\[ AveP = \sum_i precision_i\Delta recall, i\in\Omega \]

对于查询结果[🍏🍎🍍🍏🍏], \(\Omega=\{1,4,5\}\)，\(\Delta recall=1/5\)。

网上搜mAP相关教程时经常出现的图片(来自 yongyuan.name)用的就是这个公式。

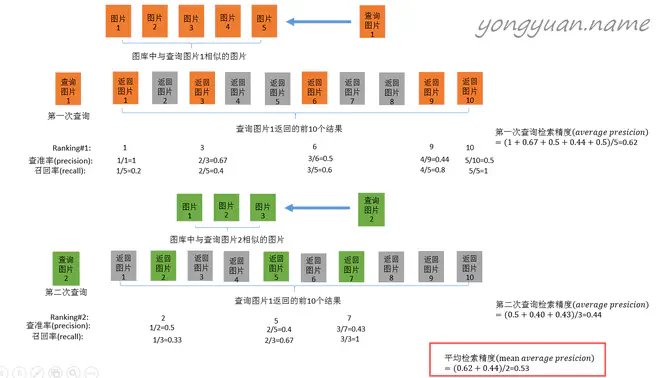
为了计算AP更精确，我们也可以用梯形面积公式替换矩形面积：

\[ AveP = \sum_{k=1}^{N}\frac{precision_k+precision_{k-1}}{2}(recall_k-recall_{k-1}) \]

同前面的讨论一致，我们也可以只计算查准点的梯形面积：

\[ AveP = \sum_i \frac{precision_i+precision_{i-1}}{2}\Delta recall, i\in\Omega \]

另外，第0个结果的查准率本来是无意义的，但是为了计算方便，补充定义\(precision_0=precision_1\)。

注意：\(precision_{i-1}\)不是\(\Omega\)集合中的上一个点的查准率，而是第i-1个查询结果对应点的查准率。

详细分析附在了文章最后。

无论是梯形还是矩形，两个公式都可以计算AP，但后一个公式精确度更高一些。

最后，平均一下每个query的AP值就得到了mAP。

\[ mAP = \frac{\sum_{i=1}^{N_q}AveP_i}{N_q} \]

水果emoji重识别任务#

再回到我提出的水果emoji重识别任务，我们来计算下两种方法的mAP：

对于Similarity1()：

query为🍏时，\(AP=\frac{1+1}{2}*\frac{1}{5}+\frac{0.33+0.5}{2}*\frac{1}{5}+\frac{0.5+0.6}{2}*\frac{1}{5}=0.393\)

query为🍎时，\(AP=\frac{0+0.5}{2}*\frac{1}{5}+\frac{0.5+0.66}{2}*\frac{1}{5}+\frac{0.66+0.75}{2}*\frac{1}{5}=0.307\)

那么\(mAP=\frac{0.393+0.307}{2}=0.35\)

对于Similarity2，同理可计算，🍎：\(AP=0.457\)，🍏：\(AP=0.307\)，\(mAP=0.382\)。

所以我们最终得到，Similarity2()优于Similarity1()。

代码实现#

相信你在理解了mAP和CMC之后，再用代码实现它俩就变得很轻松了。我最近一直在做行人重识别的项目，可以拿我一直在用的 evaluate.py中的evaluate_with_index()函数做一个参考。

One More Thing：#

我起初把\(precision_{i-1}\)错误地理解为集合\(\Omega\)的前一个值对应的准确率，因此实现代码时计算\(precision_{i-1}\)用的是下面这个公式：

old_precision = float(i) / (right_index_location[i-1]+1)

这里和一个千star级别的repo Person_reID_baseline_pytorch不一致，我还以为人搞错了，还发了一个 issue。和@ layumi讨论半天才发现我错在哪了。其实问题关键就是\(precision_{i-1}\)究竟是什么。比如当\(\Omega=\{1,4,5\}，i=4\)时，\(precision_{i-1}=precision_3\)，而不是\(\Omega\)中的前一个index 1。

正确的算法应该是

old_precision = float(i) / (right_index_location[i])

wrong.wang