什么是Diffusion模型？

Diffusion过程#

扩散（Diffusion）在热力学中指细小颗粒从高密度区域扩散至低密度区域，在统计领域，扩散则指将复杂的分布转换为一个简单的分布的过程。 Diffusion模型定义了一个概率分布转换模型\(\mathcal{T}\)，能将原始数据\(x_0\)构成的复杂分布\(p_{\mathrm{complex}}\)转换为一个简单的已知参数的先验分布\(p_{\mathrm{prior}}\)：

\[ \mathbf{x}_0 \sim p_{\mathrm{complex}} \implies \mathcal{T}(\mathbf{x}_0) \sim p_{\mathrm{prior}} \]

受到物理领域的热动力学相关知识启发，Diffusion模型提出可以用马尔科夫链(Markov Chain)来构造\(\mathcal{T}\)，即定义一系列条件概率分布\(q(\mathbf{x}_t \vert \mathbf{x}_{t-1}),\quad t\in\{1,2,3...T\}\)，将\(\mathbf{x}_0\)依次转换为\(\mathbf{x}_1\)，\(\mathbf{x}_2\)，…，\(\mathbf{x}_T\)，希望当\(T \rightarrow \inf\)时，\(\mathbf{x}_T \sim p_{\mathrm{prior}}\)。

能满足\(\mathbf{x}_{\infty} \sim p_{\mathrm{prior}}\)这个期望的\(\{q, p_{\mathrm{prior}}\}\)组合选择有很多，最简洁有效的选择就是正态分布，即：

\[ \tag{1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathrm{I}) \] \[ q(\mathbf{x}_T) = p_{\mathrm{prior}}(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathrm{I}) \quad where\ T \rightarrow \inf \]

即已知\(\textbf{x}_{t-1}\)时，\(\textbf{x}_t\)的概率分布是一个平均值为\(\sqrt{1-\beta_t}\textbf{x}_{t-1}\)，协方差为\(\beta_t\textbf{I}\)的正态分布。

根据重参数化技巧可得：

\[ \tag{2} \textbf{x}_t=\sqrt{1-\beta_t}\textbf{x}_{t-1}+\sqrt{\beta_t}\textbf{z}_{t-1} \quad where\ \textbf{z}_{t-1}\in\mathcal{N}(0, \textbf{I}) \]

这一过程可以视作\(\textbf{x}_{t-1}\)与标准正态分布噪声\(\textbf{z}\)混合，扩散率系数\(\beta_t\)控制融合\(\textbf{x}_{t-1}\)分布和标准正态分布的混合比例。从原始数据分布\(\textbf{x}_{0}\)到\(\textbf{x}_{T}\)，这一过程可以视作是在重复地给原始数据分布添加噪声，直到变为一个简单固定的分布为止。

扩散率\(\beta_t\)到底是什么呢？数据分布混合噪声分布时的比例为什么要设计成\(\sqrt{1-\beta_t}\)和\(\sqrt{\beta_t}\)呢？

假设\(\alpha_t = 1 - \beta_t\)，\(\bar{\alpha}_t = \prod_{i=1}^T \alpha_i\)，那么：

\[ \tag{3}\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\mathbf{z}_{t-1} & \text{ ;where } \mathbf{z}_{t-1}, \mathbf{z}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{\alpha_{t}(1 - \alpha_{t-1})} \mathbf{z}_{t-2}+ \sqrt{1 - \alpha_t}\mathbf{z}_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\mathbf{z}}_{t-2} & \text{ ;where } \bar{\mathbf{z}}_{t-2}, \bar{\mathbf{z}}_{t-3}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{z} \end{aligned} \]

公式中第二行到第三行的转换利用了一个性质：两个正态分布\(\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})\)和\(\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})\)相加，新分布为\(\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})\)。

将公式3写为条件概率形式，可以得到：

\[ \tag{4} q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1-\bar{\alpha}_t)\mathbf{I}) \]

由于\(\beta_t\in(0,1)\)，那么\(\alpha_t\in(0,1)\)。\(t \rightarrow \inf\)时，\(\bar{\alpha}_t \rightarrow 0\)。可以看出，\(\sqrt{1-\beta_t}\)和\(\sqrt{\beta_t}\)作为系数保证了当 \(T \rightarrow \inf\)时，\(q(\mathbf{x}_T) = p_{\mathrm{prior}}(\mathbf{x}_T)=\textbf{N}(0,\textbf{I})\)。实际上，只要\(T\)取一个足够大的值，不需要无限次迭代，得到的分布就已经很接近于标准正态分布了。

\(\beta_t \in \mathbb{R}\)具体的取值可以预先定义。原论文使用从0.0001到0.02的线性插值作为所有\(\beta\)的取值。

以上就是原数据分布到简单先验噪声分布的转换过程\(\mathcal{T}\)的描述。值得注意的是，当\(\beta_t\)预定义时，上述整个扩散过程没有出现一个可学习的参数，就可以将任意原始复杂的分布转换为简单先验分布（标准正态分布）。

下面的示意图展示了一维数据分布\(p_{\mathrm{complex}}\)中的两个样本（分别标识为蓝色和红色），经过多次加噪，最终被转换为\(p_{\mathrm{prior}}\)中的两个样本的过程。

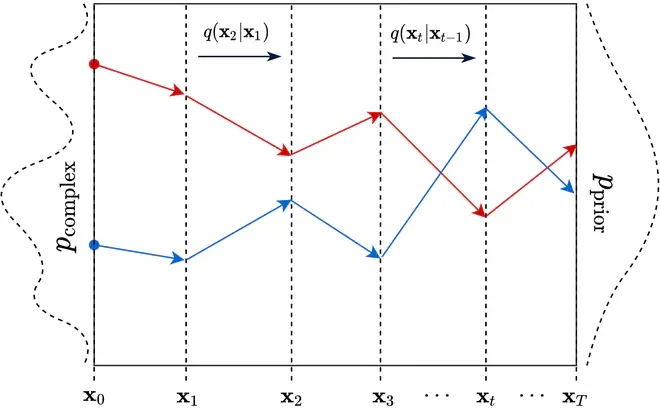
通过Diffusion模型的前向过程，复杂的分布\(p_{\mathrm{complex}}\)被转换为了一个标准正态分布\(p_{\mathrm{prior}}\)。

逆转Diffusion过程#

和GAN类似，Diffusion模型的最终目标是从\(p_{\mathrm{prior}}\)中采样一个样本，将其转换为原始数据分布中的一个样本。显然，如果逆转上一节提到的Diffusion过程，依次从\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t),\quad t\in\{T,T-1,T-2...0\}\)中采样，Diffusion模型就可以实现从\(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)到数据分布\(p_{\mathrm{complex}}\)的转换。

现在问题来了，\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)到底是什么样的分布呢？ Feller等人在1949年证明连续扩散过程的逆转具有与正向过程相同的分布形式。即当扩散率\(\beta_t\)足够小，扩散次数足够多时，离散扩散过程接近于连续扩散过程，\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)的分布形式同\(q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1})\)一致，同样是高斯分布。但是很难直接写出\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)的分布参数。为此，可以用分布\(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)来近似\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)：

\[ \tag{5} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \]

其中\(\boldsymbol{\mu}_\theta\)和\(\boldsymbol{\Sigma}_\theta\)都是要学习的函数，接受\(\mathbf{x}_t, t\)作为参数。

这样，连续迭代多次后，可以得到近似的真实数据分布\(p_\theta(\mathbf{x}_{0})\)为：

\[ \tag{6} p_\theta(\mathbf{x}_{0})=\int p_\theta(\mathbf{x}_{0:T})d\mathbf{x}_{1:T} \]

其中\(p_\theta(\mathbf{x}_{0:T})\)为\(\mathbf{x}_{0},\mathbf{x}_{1},\cdots,\mathbf{x}_{T}\)的联合概率分布。借助条件概率公式：

\[ \tag{7} p_\theta(\mathbf{x}_{0:T})=p(\mathbf{x}_T) \prod^T_{t=1}p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \]

在有了\(\boldsymbol{\mu}_\theta\)和\(\boldsymbol{\Sigma}_\theta\)后，\(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)就被确认了下来。就可以完成逆转Diffusion过程了。如下图所示：

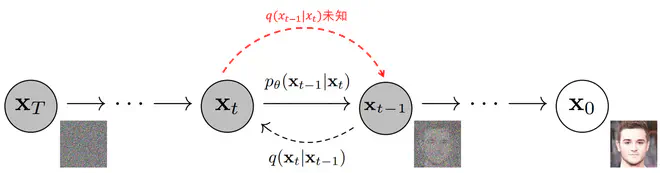
首先从\(\mathcal{N}(\mathbf{0}, \mathbf{I})\)中采样得到\(\mathbf{x}_T\)，然后在以\(\boldsymbol{\mu}_\theta(\mathbf{x}_T, T)\)为均值，\(\boldsymbol{\Sigma}_\theta(\mathbf{x}_T, T)\)为方差的正态分布中采样得到\(\mathbf{x}_{T-1}\)。依次重复这个过程，直到得到最终结果\(\mathbf{x}_0\)。由于\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)未知，所以在逆转Diffusion过程中，用学习到的\(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)代替它。

以二维平面上的一个数据集为例，原数据集中的二维数据构成了类似于字母e的一个图案，在Diffusion前向过程中，经过两次迭代，原始数据分布就被转换为了第一行第三列这样丧失了所有结构信息的分布，接近于高斯噪声分布。而逆转Diffusion过程则在\(t=T\)时刻开始，先从高斯噪声中采样，然后依次得到\(t=\frac{T}{2}\)和\(t=0\)时刻的数据分布。重建得到的分布很接近于原始数据分布，得到了一个非常不错的生成模型。

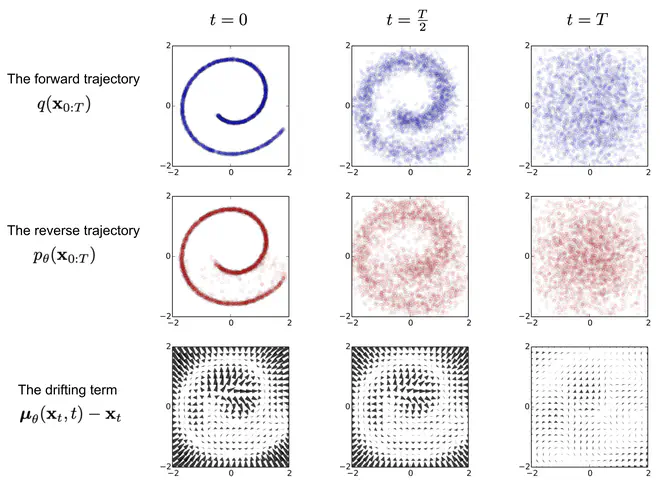
上图中还有一行值得注意，即第三行的漂移项。从\(\mathbf{x}_{t}\)到\(\mathbf{x}_{t-1}\)，实际是一个采样过程。逆扩散过程中，第\(t\)时刻的一个数据点\(x_t\)，对应于第\(t-1\)时刻\(\mathbf{x}_{t-1}\)的一个高斯分布。这听起来有些奇怪，期望逆Diffusion过程能将非结构化的噪声分布转化为结构化的数据分布，中间每一个步骤应当更”结构化“才对，怎么\(t\)时刻的一个数据点变成了\(t-1\)时刻的一个高斯分布了呢？点到分布，似乎更”乱“，更”非结构化“了。实际上，对应分布的方差\(\mathbf{\Sigma}_{\theta}(\mathbf{x}_t, t) = \sigma_t^2\textbf{I}\)，\(\sigma_t^2\)的取值很接近于\(\beta_{t}\)，即方差很小，而平均值\(\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)\)是被网络预测（可以视作一个去噪过程）得到。只要\(\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)\)预测的准，能准确的去除\(\mathbf{x}_{t}\)的噪声，就消除了分布中的“非结构化”信息。如第三列所示，\(\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)-\mathbf{x}_t\)在噪声比较大的地方（即远离原数据分布的点），值也大；而噪声小的地方，接近于0。

总结地说，Diffusion过程可以被视作在逐渐加噪声，而逆Diffusion过程则是在逐渐去噪声。学习的网络需要建模估计输入图片中的噪声。

训练目标#

现在只剩下最后一个问题，究竟怎么优化得到理想的\(\boldsymbol{\mu}_\theta\)和\(\boldsymbol{\Sigma}_\theta\)？类似于其它生成模型，可以最小化在真实数据期望下，模型预测分布的负对数似然，即最小化预测\(p_{\mathrm{data}}=q({\mathbf{x}_0})\)和\(p_{\theta}(\mathbf{x}_0)\)的交叉熵：

\[ \tag{8} \mathcal{L} = \mathbb{E}_{\mathbf{x}_0 \sim q({\mathbf{x}_0})}\big[ - \log p_{\theta}(\mathbf{x}_0) \big] \]

事实上没法写出\(p_{\theta}(\mathbf{x}_0)\)的表达式，直接计算上面的交叉熵难度很大。目前已知的仅有公式6，7以及\(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\)和\(q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\)的表达式。为此，可以做一些数学推导，将公式8中的\(p_{\theta}(\mathbf{x}_0)\)转换为已知的东西：

\[ \tag{9} \begin{aligned} \mathcal{L} &= - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \int q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} d\mathbf{x}_{1:T} \Big) \\ &= - \mathbb{E}_{q(\mathbf{x}_0)} \log \Big( \mathbb{E}_{q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \Big) \\ &\leq - \mathbb{E}_{q(\mathbf{x}_{0:T})} \log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})} \\ &= \mathbb{E}_{q(\mathbf{x}_{0:T})}\Big[\log \frac{q(\mathbf{x}_{1:T} \vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})} \Big] \end{aligned} \]

其中\(q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\)，等式变不等式那一步利用了 Jensen不等式。根据公式9，为了最小化\(\mathcal{L}\)，我们可以转而去最小化其上界\(L_{VLB}\)。

\[ \tag{10} \begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{\color{blue}{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{\color{blue}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{\color{blue}{q(\mathbf{x}_t \vert \mathbf{x}_0)}}{\color{blue}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)}} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_q [ \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} + \underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} \end{aligned} \]

上式中蓝色部分直接的变换实际上利用了贝叶斯公式：

\[ \tag{11} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \]

注意由马尔科夫链的性质，有\(q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0)=q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\)。

再重新看公式10的最后一行，可以看出\(L_{VLB}\)实际上由一个熵（\(L_0\)），以及多个KL散度(\(L_{t},t \in \{1,2,3,\cdots,T\}\))构成。其中\(L_T\)中\(\mathbf{x}_T\)和\(\mathbf{x}_0\)一个是先验分布，一个是数据分布，都是固定的，故\(L_T\)是一个常数，最小化\(L_{VLB}\)时可以忽略。可以只去研究\(L_0\)和\(L_{t},t \in \{1,2,3,\cdots,T-1\}\)。

分布\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\)和分布\(p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)\)之间的KL散度#

根据公式5，分布\(p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)\)是一个高斯分布，其平均值和方差由Diffusion模型网络预测产生。

而分布\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\)可以根据贝叶斯定律，即公式11继续推下去得到：

\[ \tag{12} \begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big) \end{aligned} \]

继续推导下去，可以发现\(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\)同样是一个高斯分布。假设：

\[ \tag{13} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I}) \]

那么，由公式12，公式13中的两个新变量：

\[ \tag{14} \begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned} \]

因此，最小化\(L_t\)这个KL损失实际上目标就是拉近下面这两个高斯分布的距离：

\[ \tag{15} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\beta}_t} \mathbf{I}) \longleftrightarrow p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) \]

多元正态分布之间的KL散度可以直接根据分布参数计算出来。

\[ \tag{16} L_t = \mathbb{E}_{q} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \|{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] + C \]

上式中\(C\)是一个不依赖于\(\theta\)的常数。为了模型简单，可以令\(\mathbf{\Sigma}_{\theta}(\mathbf{x}_t, t) = \sigma_t^2\textbf{I}\)，其中\(\sigma_t^2\)可以设置为\(\beta_t\)或\(\tilde{\beta}_t\)，论文说这两个选择效果差不多。实际上，当\(\sigma_t^2=\tilde{\beta}_t\)时，公式15中的两个分布的方差就一样了。这一选择是为了简化计算，并不是唯一的。

从公式16来看，只需要定义一个网络\(\mu_\theta(\mathbf{x}_t, t)\)，使用L2损失约束其预测值同\(\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)\)一致即可。具体来说，可以定义一个接受\(x_t\)和\(t\)作为参数的网络，从原数据分布中采样一个数据\(x_0\)，通过公式3计算得到\(x_t\)，然后利用公式14计算得到\(\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)\)，将\(x_t\)和\(t\)送入网络得到\(\mu_\theta(\mathbf{x}_t, t)\)。使用L2损失约束两个样本一致，并优化网络。

但DDPM并没有停止于此，继续分析化简公式16。\(\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)\)的输入有\(\mathbf{x}_t, \mathbf{x}_0\)，而\(\mu_\theta(\mathbf{x}_t, t)\)以\(x_t\)作为输入。借助公式3，可以得到\(\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\mathbf{z}_t)\)。将其代入，有：

\[ \tag{17} \begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\mathbf{z}_t) \\ &= \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{z}_t \Big) \end{aligned} \]

根据公式16和公式17，\(\mu_\theta(\mathbf{x}_t, t)\)在给定\(\mathbf{x}_t\)的情况下，需要预测出\(\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{z}_t \Big)\)。为了降低学习的难度，可以直接定义：

\[ \tag{18} \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) = {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{z}_\theta(\mathbf{x}_t, t) \Big)} \]

这样，公式16可以继续简化：

\[ \tag{19} \begin{aligned} L_t - C &= \mathbb{E}_{\mathbf{x}_0, \mathbf{z}_t} \Big[\frac{1}{2\sigma_t^2} \| \color{blue}{\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - \color{green}{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \mathbf{z}_t} \Big[\frac{1}{2\sigma_t^2} \| \color{blue}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \mathbf{z}_t \Big)} - \color{green}{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\mathbf{z}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \mathbf{z}_t} \Big[\frac{ \beta_t^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_t^2} \|\mathbf{z}_t - \mathbf{z}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \mathbf{z}_t} \Big[\frac{ \beta_t^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_t^2} \|\mathbf{z}_t - \mathbf{z}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{z}_t, t)\|^2 \Big] \end{aligned} \]

公式19表示在优化时，采样\(\mathbf{x}_0 \sim \mathbf{p}_{data}\)和\(\mathbf{z}_t \in \mathcal{N}(0, \mathbf{I})\)，后计算\(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{z}_t\)，然后联合时间\(t\)，送入\(\mathbf{z}_\theta\)，得到预测值，约束其与\(\mathbf{z}_t\)一致。

计算\(L_0\)#

已知\(L_0=-\mathbb{E}_{\mathbf{x}_0, \mathbf{x}_1}\log p_\theta(\mathbf{x}_{0} \vert \mathbf{x}_1)\)，而\(p_\theta(\mathbf{x}_{0} \vert \mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \sigma_1^2\mathbf{I})\)。所以\(L_0\)实际上是一个多元高斯分布的负对数似然的期望，即其熵。多元高斯分布的熵仅与其协方差有关，即\(L_0\)仅与\(\sigma_1^2\mathbf{I}\)有关，\(L_0\)是一个常数。

然而，论文DDPM指出，一般而言，\(\mathbf{x}_0\)的分布实际上是离散的，而不是连续的。比如图片数据，像素值取值必须是整数，归一化到\([-1,1]\)后，依然是离散的点。Diffusion前向的第一步实际上是为离散数据添加噪声。那么，逆Diffusion的最后一步，即从\(\mathbf{x}_1\)到\(\mathbf{x}_0\)，也不能被简单地看作从\(\mathcal{N}(\boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \sigma_1^2\mathbf{I})\)中采样，而是在从\(\mathcal{N}(\boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \sigma_1^2\mathbf{I})\)采样的基础上再加上离散化操作。\(L_0\)也不再是一个常数，而是一个与\(\mu_\theta(\mathbf{x}_1, 1)\)相关的积分，其具体表达式可以参考DDPM的Sec3.3。在忽略\(\sigma_1^2\)和边缘效应后，\(L_0\)的取值可以被\(\mathcal{N}(\boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \sigma_1^2\mathbf{I})\)的密度函数与离散时的分块大小(bin width)相乘所拟合。

另外值得一提的是，逆Diffusion的最后一步，DDPM直接取\(\mu_\theta(\mathbf{x}_1, 1)\)作为\(\mathbf{x}_0\)。

简化训练目标#

上文已经分别描述了\(L_{t},t \in \{0,1,2,3,\cdots,T-1\}\)的计算过程，最终可以按照公式10，最小化\(L_0+\sum_{t=1}^{T-1} L_{t}\)来优化网络。论文DDPM发现，去除\(L_{t}\)中的加权系数\(\frac{ \beta_t^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_t^2}\)，得到简化的训练目标如下：

\[ \tag{20} L_\text{simple}(\theta) := \mathbb{E}_{t,\mathbf{x}_0, \mathbf{\epsilon}_t} \Big[\|\mathbf{\epsilon}_t - \mathbf{z}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon}_t, t)\|^2 \Big] \]

公式中\(t\)从\(\{1,2,\cdots,T\}\)中均匀采样。\(t=1\)时对应于\(L_0\)的一个近似，\(t>1\)时对应于去除了加权系数的公式19。

相对于直接计算\(L_{VLB}\)，\(L_\text{simple}\)实现起来更加简单，\(t\)较小时的\(L_t\)权重被减少，\(t\)较大时的权重被增加。这样网络能更专注于\(t\)较大，图片中噪声更多时，更难更复杂的噪声预测任务。

训练采样流程#

可以将上文描述的Diffusion模型的训练采样过程分别总结如下：

训练时，分别从\(q(\mathbf{x}_0)\)、\(Uniform({1,\cdots,T})\)、\(\mathcal{N}(\mathbf{0},\textbf{I})\)中采样得到\(x_0\)，\(t\)和\(\epsilon\)，利用公式3计算得到\(x_t\)，将\(x_t\)和\(t\)送入网络，预测得到一个噪声。最小化预测噪声和真实采样的\(\epsilon\)之间的距离。重复这一过程直到网络收敛。

Diffusion模型的逆转采样每个时刻主要包含以下三步：

将\(x_t\)和\(t\)送入网络，预测得到噪声\(\epsilon\)
利用估计的噪声\(\epsilon\)和\(x_t\)，计算\(\mu_\theta= \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon \Big)\)
如果\(t>1\)，需要从\(\mathcal{N}(\mu_\theta, \sigma_t^2\mathbf{I})\)中采样得到\(x_{t-1}\)，利用重参数化技巧，可以将采样过程转换为首先采样\(z\in\mathcal{N}(\mathbf{0},\textbf{I})\)，然后计算\(x_{t-1}=\mu_\theta+\sigma_tz\)。如果\(t=1\)，直接令\(x_0=\mu_\theta\)

总结#

Diffusion模型的每一步推导都有严密的数学基础，调整其细节时，必须仔细思考背后的数学基础。如果它火起来，成为生成模型的主流，简直是不给我这种调参侠活路！

进一步阅读#

写本篇博客时，我主要参考了下述论文和博客文章。

wrong.wang