最近一周内,Consistency 突然成了文生图领域的热点词: Latent Consistency Model、 Latent Consistency Model LoRA (LCM-LoRA) 、 Consistency Decoder 接连出现。
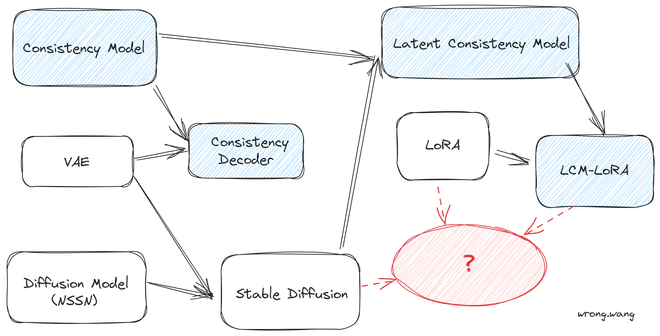
我先画了一个简单的示意图说明这些新东西和之前算法之间的关系:
- Stable Diffusion 是在预训练 VAE 空间训练 Diffusion Model 的结果。
- Consistency Decoder 是用 Consistency Model 技术训练的一个 VAE Decoder,能更好地解码 VAE Latent 为 RGB 图片。
- Stable Diffusion 经过改进后的 Consistency 蒸馏技术蒸馏后得到 Latent Consistency Model。
- 既然 LCM 是对 SD 的一个 finetune 过程,那么就可以结合 LoRA finetune 技术,不再微调整个 SD 模型,而是微调其一个 LoRA。这样就得到了 LCM-LoRA。
- LCM-LoRA 的作者发现,LCM-LoRA 可以和其它 Stable Diffusion 的风格微调模型组合,依然起效,可以实现免训练的加速各种 SD 微调模型。这些 SD 模型,有了 LCM-LoRA 之后,什么都不用做生成却快了十倍。
在心里大概明确 SD、CM、LCM、LCM-LoRA 之间关系后,下面听我来依次讲一下我对这些带“Consistency”的新算法的理解。
Consistency Model#

Consistency Model 在 Diffusion Model 的基础上,新增了一个约束:从某个样本到某个噪声的加噪轨迹上的每一个点,都可以经过一个函数 \(f\) 映射为这条轨迹的起点。 显然,同一条轨迹上的点经过 \(f\) 映射结果都是同一个点。这也是训练 Consistency Model 时所使用的损失约束。
当微调 Diffusion Model 使其满足 Consistency 约束之后,其采样生成的过程就非常自然。从噪声中采样一个点,送入 \(f\) 中,就得到了其对应的数据样本。这就是 Consistency Model 的单步生成模式。与此同时,Consistency Model 也可以通过多步生成来实现牺牲速度提升生成质量的权衡。Consistency Model 的多步生成过程大略如下图所示:

形式化地讲,我们常用的 Diffusion 模型实际上是训练了一个网络 \(\textbf{s}_{\phi}(x, t)\) 拟合 \(\nabla{log(p_t(x))}\),然后 Diffusion 的采样过程可以理解为给定 \(x_{T} \sim \textbf{N}(\textbf{0}, \textbf{I})\),有
\[ \frac{\mathrm{d}x_t}{\mathrm{d}t} = -t\textbf{s}_{\phi}(x_t,t) \]给定起始点,给定每个点的梯度后,通过迭代计算得到 \(x_{\epsilon}\),其中 \({\epsilon}\) 是一个小正数(比如 EDM 中使用的 0.002)。用 \(x_{\epsilon}\) 当作采样得到的样本。这里引入 \({\epsilon}\) 是为了避免在 \(t=0\) 处易出现的数值不稳定。
Consistency 在 Diffusion 的基础上,继续定义一个一致性函数 \(f: (x_t, t) \rightarrow x_{\epsilon}\)。一致性函数具有两个最关键的特性:
- \(f( x_{\epsilon}, \epsilon) = x_{\epsilon}\)
- 任意 \(t_1,t_2\in [\epsilon, T]\) 满足 \(f(x_{t_1}, t_1) = f(x_{t_2}, t_2)\)。
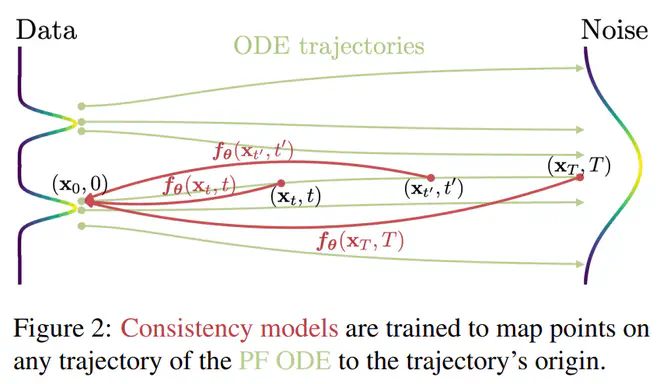
Consistency Model 的目标是找到一个 \(f_{\theta}\),能满足上面这两个条件,来拟合 \(f\)。在得到了一个合理的 \(f\) 的近似 \(f_{\theta}\) 后,就可以调用下面的采样算法从噪声生成样本了:

参考 EDM,Consistency Model 干脆设计 \(f_{\theta}(x,t)=c_{skip}(t)x+c_{out}(t)F_{\theta}(x, t)\),其中 \(c_{skip}(t)\) 和 \(c_{out}(t)\) 被定义为
\[ c_{skip}(t)=\frac{\sigma^2_{data}}{(t-\epsilon)^2+\sigma^2_{data}},c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{t^2+\sigma^2_{data}}} \]显然,当 \(t=\epsilon\) 时,这个设计下的 \(f_{\theta}\) 一定能满足一致性函数的第一条性质。
那么第二个性质怎么去拟合呢?难道是随机从轨迹中采样两个点,送入 \(f_\theta\) 约束其相同吗?
在我们已经有一个训练收敛的 Diffusion Model 时,可以通过最小化下面这个损失来去拟合第二个性质:

即从样本集中采样一个样本,加噪变为 \(x_{t_{n+1}}\),然后利用预训练的 Diffusion 模型去一次噪,预测到另外一个点 \(\hat{x}_{t_n}^{\phi}\)。然后计算这两个点送入 \(f_{\theta}\) 后的结果,用特定损失函数约束其一致。
这里的预测过程形式化地写就是,已知 \(\textbf{s}_{\phi}(x, t)\) 和 \(\frac{\mathrm{d}x_t}{\mathrm{d}t} = -t\textbf{s}_{\phi}(x_t,t)\),用 ODE Solver \(\Phi\) 去解这个 ODE:
\[ \hat{x}_{t_n}^\Phi = x_{t_{n+1}} + (t_n - t_{n+1})\Phi(x_{t_{n+1}}, t_{n+1};\Phi) \]比如常用的 Euler solver 就是 \(\Phi(x,t;\phi)=-t\textbf{s}_{\theta}(x,t)\) 。DDIM、DPM++我们常听的词都是 ODE Sovler 的一种。
Consistency Model 论文附录证明了,当最小化 \(\mathcal{L}_{CD}^N\) 为 0 时,\(f_\theta\) 和 \(f\) 的误差上确界足够小。所以,通过最小化 \(\mathcal{L}_{CD}^N\) 就能让 \(f_\theta\) 和 \(f\) 足够接近。

这里再补充几个关键细节:
- \(f_{\theta}(x,t)=c_{skip}(t)x+c_{out}(t)F_{\theta}(x, t)\) 中的 \(F_\theta\) 就是给定 \(x_t\),\(t\) 去预测一个 \(\hat{x}_0\)。之前各种不同的 Diffusion 模型预测结果都可以转变为预测 \(x_0\)。由于 \(c_{skip}\) 很快收敛于 0,\(f_{\theta}\) 其实基本由 \(F_\theta\)(即 Diffusion 模型预测的 \(\hat{x}_0\)) 决定。
- 计算 \(\hat{x}_{t_n}^{\phi}\) 对应的轨迹起点时用的网络的参数是 \(\theta\) 的滑动平均(EMA)。作者认为这样可以稳定训练过程,提升最终训练效果。
- 判定两个点的 \(f_{\theta}\) 预测结果是否一致时使用的损失函数可以是 MSE、LPIPS 等等损失,实际上,针对自然图片的损失 LPIPS 在 Consistency Model 的训练过程中取得了最好的结果!
应该怎么理解这一训练过程呢?在研究数学上的证明之外,我提供一个可能不是那么严谨的直觉理解,如果有问题,欢迎指出。

如上图所示,给定某个样本 \(x_0\),经过 Diffusion 前向加噪过程得到 \(x_{t_{n+1}}\),Diffusion Loss 是约束根据 \(x_{t_{n+1}}\) 送入网络后的输出计算得到的 \(\hat{x}_0\) 与真正的 \(x_0\) 一致。Consistency Model 则要求根据这个预测得到的 \(\hat{x}_0\) 和 \(x_{t_{n+1}}\),执行一次 Diffusion 去噪过程得到 \(\hat{x}_{t_n}\),然后继续预测 \(\hat{x}_0\),要求这两个预测 \(\hat{x}_0\) 一致。显然 Consistency Loss 是对 Diffusion Loss 的一个加强(或者可以说,更高一阶?):基于预测值再预测一个结果,要求第一次预测值与第二次预测值之间差异足够小。
我数学不太好,但感觉这种最小化两次累积预测误差的思路似乎和解 ODE 的数值计算方法(或者优化算法)里面的什么 “多走一步,计算累积误差” 之类的思路异曲同工之妙。不知道有没有人能替我懂我在说什么…
这里有个小疑问,如果 Diffusion Loss 能接近 0,那么 Consistency Loss 也能接近 0;反过来还成立吗?
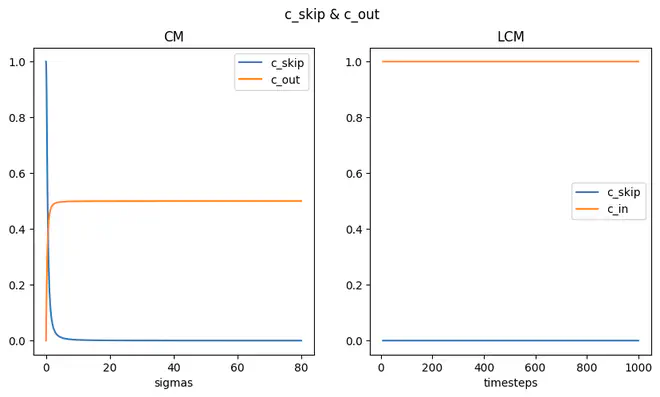
当然,上面的理解是有偏差的,比如要用 \(c_{skip},c_{out},x\) 组合计算才能得到 \(f_{\theta}\)。但是我把 diffusers 中 LCM 和 CM 中的 get_scalings_for_boundary_condition 函数实现结果可视化了一下:
分析完从预训练 Diffusion Model 构建 Consistency Model 过程,我产生了几个疑问,不知道未来能不能回答:
- 用 Consistency Loss 去优化的同时,再增加 Diffusion Loss 会有什么帮助吗?毕竟 Consistency Loss 建立在得分估计网络足够准之上,只用 Consistency Loss 会降低其准确性吗?增加 Diffusion Loss 帮助维持得分估计网络的准确性有用吗?
- 从理论上理解,CM 的训练过程中每一步都在预测 \(x_0\),作者也指出可以用 LPIPS Loss 这样的专门针对 RGB 图片的,没有对带噪声结果特殊优化过的 Feature Match Loss 来优化 CM,那么是不是意味着可以把 GAN 领域之前常用的什么 VGG Loss 之类的一整个 loss 调参生态再加回来了?比如增加什么 ArcFace Loss 来约束生成人脸一致,做保人脸 ID 特征的下游应用…
Latent Consistency Model#
Latent Consistency Model(LCM)是在 Stable Diffusion 的基础上新增 Consistency 约束蒸馏的结果。LCM 是 CM 在文生图领域的一个应用,它以 Consistency Model 作为理论基础,在 Consistency 蒸馏的过程中引入了 Classifier Free Guidance(CFG)增广,也设计了 skipping-step 这样的策略来加速蒸馏收敛。
在理解 Consistency Model 后,再看 LCM 的训练过程就没有那么难懂了,我们直接看 LCM 具体的蒸馏过程:

蓝色部分是 LCD 相对于 CD 新增的部分。LCD 多了一个 VAE 编码过程 \(E(\cdot)\)、多了一个 CFG 常用的 Guidance Scale 的范围 \([w_{min},w_{max}]\)、多了一个表示 Diffusion 去噪过程跳步大小的参数 \(k\)。
下面详细描述下 Latent Consistency Distillation 的蒸馏过程,我会着重强调与 Consistency Model 中描述蒸馏算法的不同:
- 采样当前一次训练所需要的数据: 从数据集中采样的样本变为了 \((z, c)\),即图片 latent 与图片 caption。SD 加噪过程共有 \(N=1000\) 步,从 \(1\) 到 \(N-k\) 中采样当前训练所针对的 timestep \(n\),即当前一个 sample \((z, c)\) 选择了 \(z_{n+k}\)、\(\hat{z}_{n}\) 这两个点去计算 Consistency 约束 loss。最后从 \([w_{min},w_{max}]\) 中选择一个 \(w\) 作为后续预测 \(\hat{z}_n\) 时使用的 Guidance Scale
- 加噪: 用标准的 Diffusion 加噪算法计算 \(z_{n+k}\),计算了加噪轨迹上的一个点
- 执行一次熟悉的 Diffusion 去噪过程: 以前 Stable Diffusion 不是在一个循环里重复去噪过程嘛?当前这步就是重复一次之前的去噪过程,可以用 DDIM、DPM Sovler++之类熟悉的 Diffusion Scheduler 完成这一步。在这一步的预测中,融合了 CFG 的 Guidance Scale,即在 Consistency Distillation 的蒸馏算法后多增加一项 \(w\) 倍的 Positive Prompt 减 Negative Prompt 这样熟悉的东西。另外,为了加速训练收敛,LCM 的作者也提出在这一步没必要只做一步 \(z_{n+1} \rightarrow z_{n}\) 这样的预测,而是可以用 DDIM 之类的算法,直接完成 \(z_{n+k} \rightarrow z_{n}\) 的预测。
- 计算一致性蒸馏损失:上一步得到了一个加噪轨迹上的点,以及其用 Diffusion 去噪算法预测得到的另外一个点。这一步就是分别用当前网络权重以及网络权重的 EMA 计算两个点对应的一致性函数输出,然后用一个损失函数约束输出一致。
- 更新网络权重
- 计算网络 EMA
LCM 的实验分析了一下第三步去噪算法中不同组件的选择对收敛的影响:
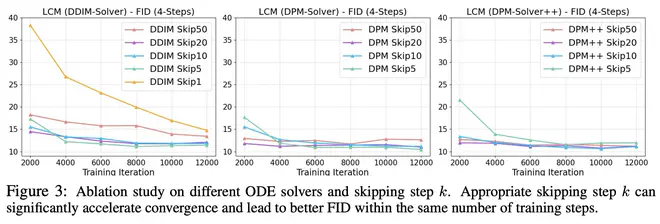
比如,在 \(k\) 足够合理时,只需要 2000 步迭代,LCM 4 步采样的 FID 就已经基本收敛了。观察 DDIM 那个子图,可以发现当 \(k=1\) 即没有 skipping-step 技巧时,收敛很慢;但是当 \(k=50\) 时,FID 也一直很高,说明一下子跳过太多步时,DDIM 解 ODE 的误差太大了。但是 \(k=50\) 时,DPM 和 DPM++收敛还是正常的。这个实验的结果和我们之前的积累的经验是吻合的:\(k=50\) 对应于之前 Stable Diffusion 推理时迭代 20 次,此时 DPM++和 DPM 的表现确实比 DDIM 强。
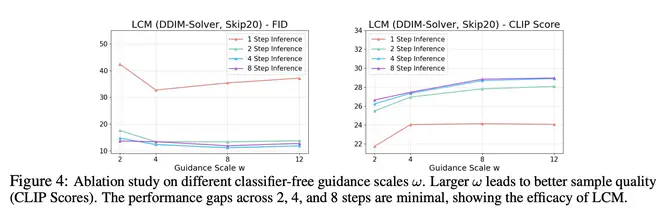
对于 Guidance Scale 的选择,LCM 作者用不同 LCM 的迭代次数与不同 Guidance Scale 做了对比。发现 \(w\) 增加有助于提升 CLIP Score,但是损失了 FID 指标(即多样性)的表现。另外,LCM 迭代次数为 2、4、8 时,CLIP Score 和 FID 相差都不大,说明了 LCM 的蒸馏性能确实非常强悍,两步前向的效果可能都足够好了,只是一步前向的结果还差些。


LCM-LoRA#
LCM 论文出来后,社区的关注度其实也没有那么高。但后面 LCM 作者开源了代码,很多人开始在 twitter 上惊呼这是第一篇开源了代码和模型的 Diffusion 蒸馏文章,还用了 OpenAI 的 Diffusion 祖师爷的新生成模型 Consistency Model 的思路。社区对 LCM 的关注度一下子就上去了。
但 LCM 也有问题呀,LCM 需要微调整个 SD 模型,社区里那一堆 SD finetune 模型难道每个都得再优化一下吗?这时 LCM 的作者和 Huggingface Diffusers 的作者就合作搞了 LCM-LoRA 出来。
既然 LCM 也只是一个对 SD 的一个微调过程,只是换了一个 Loss 嘛,那自然可以借助 LoRA 的力量,给 SD 外挂一个 LoRA 组件,只用 LCM 的蒸馏损失优化 LoRA 挂件的权重。这样就得到了 LCM-LoRA。
如下图,LCM-LoRA 作者发现,LCM-LoRA 可以和现在社区里的各种 LoRA 模型组合,共同作用,得到既能加速,又有风格的自定义 LCM 模型。
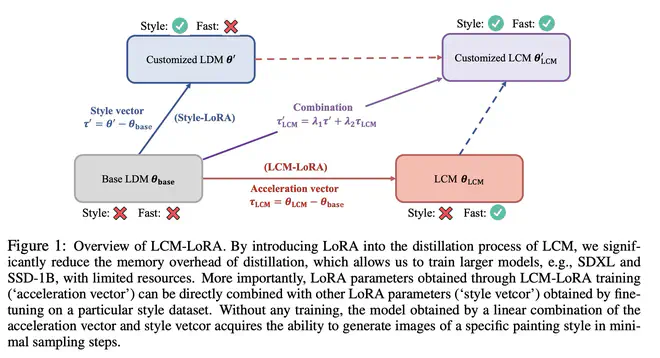
LCM-LoRA 为啥能随便和之前各种提供 Style 的 SD LoRA 直接加权使用呢?
- 从模型角度出发,LoRA 本身就是把 finetune 增量矩阵限制成了低秩矩阵,两个低秩权重增量矩阵做加权冲突的程度没那么大,这是 LoRA 本身的优良性质。
- 从数据分布角度讲,微调过程中 Diffusion 前向的数据分布没有改变,顶多是子集的差异,LCM-LoRA 训练过程中依然用到了 Diffusion 去噪,保证模型输出也不会偏移原分布太多,从 \(z_{n+k}\) 预测的 \(\hat{z}_n\) 依然接近真实 \(z_n\) 的分布。
- 从我这种实验算法工程师的角度讲,LCM-LoRA 就训练了那么几 M 样本,网络模型又那么多冗余权重,没有那么脆弱,还没遗忘之前的东西罢了。另外可能只是结果没那么差罢了,在 Style LoRA 的训练数据集上再微调下 Style LoRA 和 LCM-LoRA 肯定能有更好的效果。
我自己也测试了一下 LCM-LoRA 的效果在我们内部的保人脸 ID 项目上的效果,直接让一张图从 2.8s 生成变成了 0.4s 生成,结果还很惊艳:

还用 7.5 肯定是不行的,我替你淌过坑了。
另外,由于 LCM-LoRA 训练不太耗资源,如果对 LCM-LoRA 训练时 Guidance Scale \(w\) 的取值范围不太满意,或者想直接把 Negative Prompt 蒸馏进 LoRA,那都推荐改下 diffusers 开源的脚本自己微调一下 LCM-LoRA。
Consistency Decoder#
Consistency Decoder 是 OpenAI 训练的一个以 Stable Diffusion 中所使用的 VAE 的 Latent 作为 condition 的 Consistency Model。什么训练细节 OpenAI 全部没说,甚至模型定义都是隐藏在权重文件中,由社区重定义的。这个模型在 OpenAI 的 DALLE3 介绍论文中提到过,我之前写过那篇论文的解读: Improving Image Generation with Better Captions - wrong.wang,其中也提到了它。
Consistency Decoder 是可以和 LCM-LoRA 结合使用的,只是提供了一个 latent 解码为 RGB 的新选择。我同事测试了一下 Consistency Decoder 的效果,推理慢了很多,效果提升没有想象的那么明显。
总结#
LCM-LoRA 真正做到了什么都不用做,即插即用,就能让开源社区里基于 SD 的生态的模型取得几倍的速度加成。从 CM、LCM 到 LCM-LoRA 这一系列改进让我看到了什么叫做集思广益,文生图领域一日千里。正如本篇文章头图里的红色区域,当 LCM-LoRA 和 Stable Diffusion 生态相遇,会在应用端产生怎样的化学反应呢?让我们拭目以待!
这一系列 Consistency Model 背后涉及到很多理论推导,我数学不行,如果您发现我上面的叙述中有哪些不对,请评论说明,互相交流学习。
当然,写作不易,还是请大家多多表扬我!哈哈。